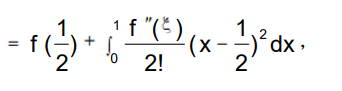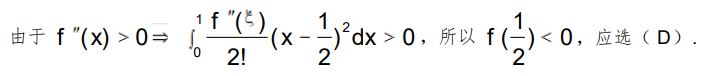设函数f(x)在[0,1]上二阶可导。且,则（）-查字典考试网

设函数f(x)在[0,1]上二阶可导。且,则（）

收藏

设函数f(x)在[0,1]上二阶可导。且,则（）

A、
B、
C、
D、

查看答案

正确答案：

D

答案解析：

有高于一阶导数的信息时，优先考虑“泰勒展开”。从选项中判断，展开点为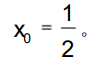

将函数f（x）在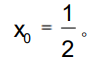出展开，有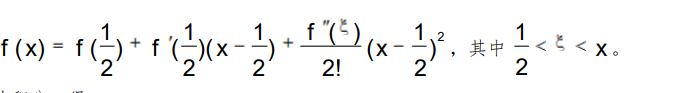

两边积分，得

上一题下一题

你可能感兴趣的试题

下列矩阵中阵，与矩阵相似的是

A、
B、
C、
D、

查看答案

求函数u=ln(2x+3y+4z²)的全微分du。

查看答案

二重积分定义式中的，λ代表的是

A、小区间的长度
B、小区域的面积
C、小区域的半径
D、以上结果都不对

查看答案

曲线y=x²+2inx在其拐点处的切线方程为。

查看答案

二元函数z=sin(2x+3y)，则

查看答案

热门试题更多>

试卷库

试题库